引言：本文是数据智能系列的第四篇。前三篇文章（ 《数据智能时代来临：本质及技术体系要求》《多维度分析系统的选型方法》《我们理解的数据中台》）分别阐述了数据智能体系构建的技术要求，对团队工作中涉及到的多维度分析系统的选型方法进行了穿插介绍，以及对我们理解的数据中台进行了阐述。按照原先的规划，接下去的内容会涉及数据智能平台的数据治理、安全计算以及质量保障等方面。结合当前大环境，今天就数据的安全计算体系进行分析。

 

1    大数据行业对于数据融合的需求和痛点

1.1    向数字时代迈进的趋势不可逆转

 

从第一台计算机的问世，到互联网的诞生，再到近十年来移动互联网的蓬勃发展，整个世界的数字化进程已经呈现出越来越迅速、清晰的趋势。使用各类APP、电子商务、电子支付等已经成为我们的习惯。

近年来，5G技术日益成熟，其核心场景包括：增强移动宽带(eMBB)，面向VR/AR、超高清视频等需要高速大流量的移动宽带业务；大规模机器类通信(mMTC)，面向大规模物联网等业务；超高可靠及低延迟/时延(uRLLC)，面向无人驾驶、工业自动化等业务。^[1]

 

 

显然，我们将进入万物互联的时代，万物互联也就意味着万物皆数。数字世界将是这个物质世界的孪生世界，这种趋势不可逆转。

 

1.2    数据是资源更是资产

 

 数字时代的各种产品和服务除了为公众提供直接价值外，还产生了大量的数据。由于数据特殊的选择价值的存在，数据不仅对个人意义重大，还日益成为现代商业的核心价值与重要资产。数据正在重新塑造人类生活的方方面面，包括金融、广告、零售、医疗、物流、能源和工业等。

随着人工智能时代的到来，数据在现代商业活动中也成为了最重要的竞争资源之一。各个巨头公司利用自身数据优势建立起行业壁垒。例如，有些打车软件公司拥有用户日常出行数据，包括乘客的起点与终点。他们可以利用这些数据来优化自己的产品和业务，甚至可以用这些数据来进行预测，比如房地产价格指数或者政府道路优化方案等。

上面的例子深刻体现了大数据的扩展价值，还有一个更广阔的价值是大数据的融合价值，也就是数据的总和比部分更有价值。当我们将多个数据集的总和重组在一起时，重组总和的价值比单个总和的价值更大。譬如在普惠金融方面，中国人民银行征信中心通过以往用户在金融机构中的借贷行为形成了一部分人的信用数据，但是这类人群占社会总人口的比例很小。如果我们想让更多人享受到普惠的金融服务，就需要针对不同人群设计不同产品，而这就需要更多的数据进行信用的积累，包括电商、消费、社交等数据。

 

1.3    隐私保护是自由的基础 ^[2]

 

在互联网、人工智能给我们带来便利的同时，也存在一些乱象。因此，保护用户隐私的需求也变得越来越迫切。

技术使人类能够更尊重和更好地保护彼此的权利。同样的，技术也可能让人类能够有更多的新方式侵害彼此的权利。有 “摩尔定律” 也有了 “摩尔的不法之徒定律”， 垃圾信息传播者、身份盗窃者、在网上“ 钓鱼”的罪犯、间谍、僵尸网络入侵者、黑客、网络恶霸、数据敲诈者，他们给互联网带来的负面影响也非常大。

2018年5月25日正式生效的欧盟通用数据保护条例（GDPR）引起全球广泛关注，这部被称为“史上最严”的数据保护法案对科技行业和个人生活产生了深远影响。它是人类历史上第一个规定个人数据所有权规则的条例，它在法律上明确规定了个人数据是归个人所有的数据资产。

同样的，近两年来，中国对于个人隐私保护和数据安全方面在立法和执法力度上都在持续加大。这些法律法规将保障人们对个人数据有更多的掌控权。

 

2    行业对于解决痛点方面的探索

2.1    行业痛点

 

数据的融合可提高其价值，数据的交叉使用会产生协同作用。

但因为数据本身的可复制性和易传播性，若一经分享无法追踪使用情况，数据资产的分享与协同开发受到严重制约。此外，我们的数据需要得到保护和隔离，然而数据对人类社会的价值在于联合在一起的计算和分析，这就构成了一对矛盾关系。

虽然个人对隐私的保护、商业公司对数据的保护，都是正当的利益诉求，但却产生了一个个数据孤岛——拥有数据源的中小企业无法安全地将数据共享或变现。而包括大数据公司、开发者和科学家在内的数据使用者仅能接触到有限且费用高昂的数据集。与运营商等大数据源的合作需要开发人员在现场将模型部署于数据源的服务器上，模型算法存在泄露风险，且效率低下。

 

受保护的数据如何产生价值 ? 这是目前大数据产业发展的最大痛点。可以毫不夸张地说，如果这个矛盾和问题得不到解决，大数据产业的发展将受到极大制约。

为了解决被保护的数据如何产生价值这个问题，并且能够在此基础上，充分发挥大家的积极性，创造更大的协同价值，业内同仁在安全计算、价值网络和区块链的结合等多个方面进行了探索。有机会我们再针对价值网络、区块链等方面单独成文介绍。

 

2.2    模式探讨

 

任何解决方案，必定都是针对某个问题，找到收益较大化、弊端较小化的最优解，而不可能十全十美。一切追求完美的方案必定是和现实相冲突的。就数据资产的处理而言，我们主要需要考虑三个因素：便利性、安全状况和成本。所以对于不同模式的讨论，也可以简化为对于这三个因素的平衡。

 

 

模式一： 中立国模式

 

这种模式主要适用于其中一方数据相对丰富的情况，譬如有政府、互联网公司等参与的情况。在这里我们可以称这些拥有丰富数据的一方为主体数据提供方。主体方拥有大量的、覆盖面广且基础属性全的数据；数量众多的需求方拥有自己的小价值数据，同时对于这些数据有扩量、统计层面的强烈需求。由于主体数据提供方的数据量非常庞大，不易轻易搬动，这些数据一般相对固定，并作为数据主板。而众多数据使用需求方因为数据体量小、数据传输方便，可以比较便利和更低成本地为数据需求方提供服务。

这样的服务可以通过一个具有公信力的独立第三方来搭建中立国环境，包括数据存储、大数据计算以及安全环境，并通过沙箱、数据安全技术、审计手段等确保数据使用过程中的合法合规及安全隐私保护。目前也已经有不少公司提供这样的服务，如浙江省数据安全服务有限公司等。

 

模式二：领事馆模式

 

这种模式是中立国模式的变种。该模式系统不是由独立第三方进行搭建，而是由数据主体方提供，然后划出一块区域，让数据需求方独立搭建自己的计算环境。主体方数据通过某种方式能够让数据需求方接触到并参与计算，但是因为“领事馆”还是在数据主体方的整体环境中，所以数据的流进流出会受到主体方的监管, 特别是需要流出的数据，须满足数据主体方的审计标准，保证数据合法合规并受到隐私保护。这种模式主要从主体方数据安全考虑，但没有中立国模式便利，成本也相对较高。目前，一些互联网大数据公司已经采用领事馆模式。

 

模式三：安全多方计算和联邦计算模式

 

  该模式主要适用于这种情况：在数据拥有方因为政策、数据价值高无法出库等要求下，数据无法进行直接流动，同时又对于外部数据有非常强烈的使用需求。该模式考虑更多的是数据安全问题，对于技术方面的要求也更强、更具有挑战性，但对于便利和成本方面的考虑就不是那么突出了。当然这种模式也可以与前两种模式结合使用，但成本也会更高。

目前已经有不少创业型的公司在提供相关的产品和平台，部分大数据科技公司也会自主研发。

 

 

2.3    安全计算技术研究

2.3.1    安全多方计算

 

安全多方计算（MPC：Secure Muti-Party Computation）研究由图灵奖获得者、中国科学院院士姚期智教授在1982年提出。姚教授以典型的百万富翁问题来解释安全多方计算。

百万富翁问题指的是，在没有可信第三方的前提下，两个百万富翁如何不泄露自己的真实财产状况来比较谁更有钱。通过对这个问题的研究，姚教授形象地说明了安全多方计算面临的挑战和解决问题的思路。经Oded Goldreich、Shaft Goldwasser等学者的众多原始创新工作，安全多方计算逐渐发展成为密码学的一个重要分支。

具体而言，MPC 指的是用户在无须进行数据归集的情况下，完成数据协同计算，同时保护数据所有方的原始数据隐私，而参与各方在将数据保留至各自本地的情况下，执行共同的既定计算逻辑（算法），得到计算结果。数学形式化语言描述为：有n个计算参与方，分别持有私有数据x1, x2, …, xn，共同计算既定函数f(x1, …, xn)，得到正确的计算结果。计算完成后，参与各方除了自己输入的数据和输出的结果外，无法获知任何的额外信息。

MPC 协议满足的基本特性是：

• 输入隐私性：协议执行过程中的中间数据不会泄露双方原始数据的相关信息；
• 健壮性：协议执行过程中，参与方不会输出错误的结果。

这两点保证了数据流通过程中所需满足的基本要求。

 

接下去我们针对 MPC 做一个简要描述，不对细节进行过多展开。

根据计算参与方数量的不同，MPC可分为只有两个参与方的2PC和多个参与方（≥3）的通用MPC。

安全两方计算所使用的协议为混淆电路(Garbled Circuit - GC)+不经意传输(Oblivious Transfer - OT)；而安全多方计算所使用的协议为同态加密(HE) + 秘密分享(Secret Share - SS) + OT。

 

2.3.2    混淆电路-GC

 

我们知道，任意函数在计算机语言内部最后都是由加法器、乘法器、移位器、选择器等电路表示，而这些电路最终都可以仅由AND和XOR两种逻辑门组成。一个门电路其实就是一个真值表，比如AND门的真值表就是：

 

 

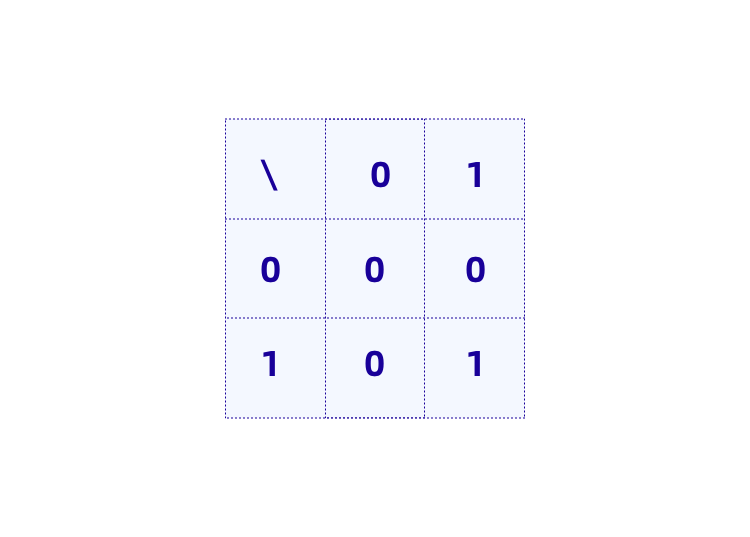
例如其中输入表示两根输入线，那么当两个输入(wire)都取1时，输出wire=1：即 1 AND 1 = 1。 如果只是把函数变成这样的输入是 0/1的电路，数据是没有办法起到保护作用的，因此需要对输入的这些0/1进行加密。

假设我们把每个wire都使用不同的密钥进行加密，并把真值表更改为：

 

 

以上图右下角作为例子，我们选取随机标签b和d (安全参数为k的比特串)代替简单的比特1，输出为加密的f，加密密钥是b和d。这个门从控制流的角度来看还是一样的，只不过输入和输出被加密了，且输出必须使用对应的输入才能解密，解密出的f又可以作为后续门的输入。这种加密方式就称为“混淆电路”。^[4] 

通过对电路中所有的门按顺序进行加密，我们得到了一个用GC表示的函数。这个函数接收加密输入并输出加密结果。

 

现在我们假设有两个参与方，Alice(简称A)和Bob(简称B) 。他们分别提供数据a、b，并希望安全计算约定的函数为F(a,b)，那么一种基于GC的安全两方计算协议过程可以非正式地描述如下：

• A把F进行加密，得到GC表示的函数GC-f; （注意这里A是电路的生成者，因此他了解每根wire的密钥）；
• A把自己输入的a用第1步中对应的wire密钥加密，得到Encrypt(a)；
• A将Encrypt(a)、GC-f一并发送给B；
• A将B输入的b使用第1步中对应的wire密钥加密，得到Encrypt(b)，并将Encrypt(b)发送给B；
• B拥有完整的GC和输入，因此可以运行电路得到加密的输出；
• A把输出wire的密钥发给B，B解密后得到最终结果F(a,b)；
• 如果A需要，B再把F(a,b)发给A。

 

以上步骤存在一个BUG：第4步中，A怎么可以接触B输入的b呢？这显然违背了安全多方计算的原则。这里就需要使用下面介绍的不经意传输(OT)协议。

 

2.3.2.1    不经意传输-OT

 

Alice扮演传输中的发送者（Sender），Bob扮演传输中的接收者(Receiver)，目的是让B从A处得到Encrypt( b)，A无法知道b的内容。

 

 

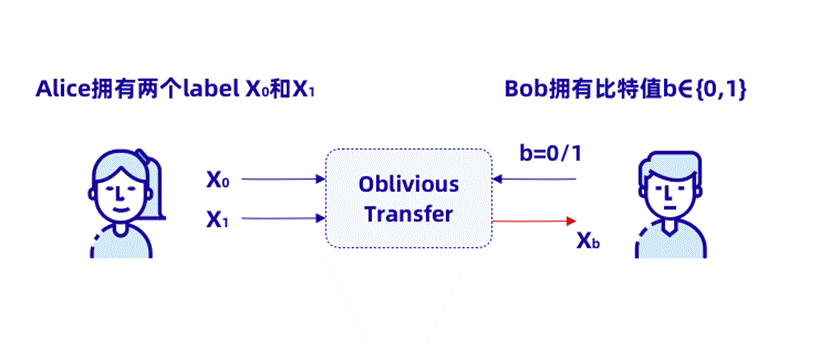
如上图所示，Alice 知道每个 Wire 的加密编码 X0, X1。 Bob需要根据自己的比特来获知对应的编码，如果是0就获得 X0, 如果是1就获得 X1, 同时不让 Alice 知道这个 b 的具体内容。整个过程没有第三方参与。

具体过程可以非正式地描述如下：

• A 生成一个随机数 n, B 生成一个随机数 m
• A 将 N = gⁿ (g的n次方) 发送给 B, B 将 M = g^m  (g的m次方)发送给 A, 其中 g 是一个双方设定的安全参数值。这样 A 就拥有了 n, N, M 三个值
• A 计算 K0= Hash(Mⁿ) ， K1=Hash((M/N)ⁿ)
• A 将 K0 作为密钥加密标签 X0, 以 K1作为密钥加密 X1: e0=Encrypt _k0(X0), e1 = Encrypt _k1(X1), 然后将 e0和e1发送给B
• B 收到 e0、e1 后，已知 Mn = Nm, 所以可以用 Nm来计算出 K0, 然后用 K0就可以解密出 e0, 但是无法解密出 e1
• 如果 B 希望能够获得对应的 X1, 那么只要把第三步里面的 M 变成 N*gm, 这样在 K1 的计算中就变成了 K1 = Hash( Nm ), 从而能够解密 X1, 但无法解密 X0

 

2.3.3     同态加密-HE

 

我们先来看下图。

 

 

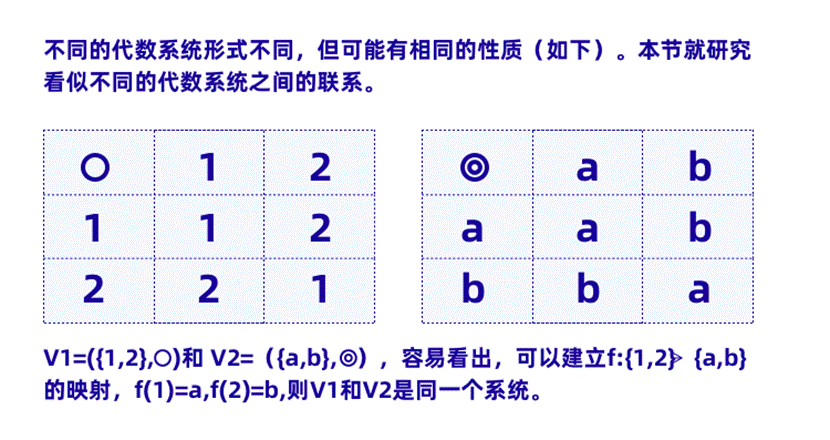
不难发现，左边的代数系统和右边的虽然操作符号不同，但规则是相同的。这就是所谓的两个系统是同态的。我们只要找到一个函数 f, 能够把左边的数据集 {1,2} 映射到 {a,b}, 那么左边的运算就可以转换为右边的运算。得到运算结果后，我们就可以通过逆变换转换回左边的值。

比较正式的描述是：

• 如果我们有一个加密函数f , 把明文A变成密文A’, 把明文B变成密文B’，也就是说f(A) = A’ ，f(B) = B’ 。另外我们还有一个解密函数  ，能够将 f 加密后的密文解密成加密前的明文。
• 对于一般的加密函数，如果我们将A’和B’相加，得到C’。我们对C’进行解密得到的结果一般是毫无意义的乱码。
• 但是，如果f 是个可以进行同态加密的加密函数， 我们对C’进行解密得到结果C， 这时候的C = A + B。

这样，数据处理权与数据所有权可以分离，企业在防止自身数据泄露的同时，还可以利用云服务的算力。

 

同态加密的类型：

a) 如果满足f(A)+f(B)=f(A+B)， 我们将这种加密函数叫做加法同态

b) 如果满足f(A)×f(B)=f(A×B)， 我们将这种加密函数叫做乘法同态

 

如果一个加密函数f只满足加法同态，就只能进行加减法运算；

如果一个加密函数f只满足乘法同态，就只能进行乘除法运算;

如果一个加密函数同时满足加法同态和乘法同态，则称为全同态加密。那么使用这个加密函数可以完成加密后的各种运算(加减乘除、多项式求值、指数、对数、三角函数)。

加法和乘法同态加密的难题目前都已解决，但要想实现全同态加密就比较困难了。不过好消息是： 2009年，Gentry，一个斯坦福大学的博士生，基于理想格提出了一个全同态加密方案。

 

2.3.4     秘密分享-SS

 

为了说明什么是秘密分享，我们先看下图：

 

 

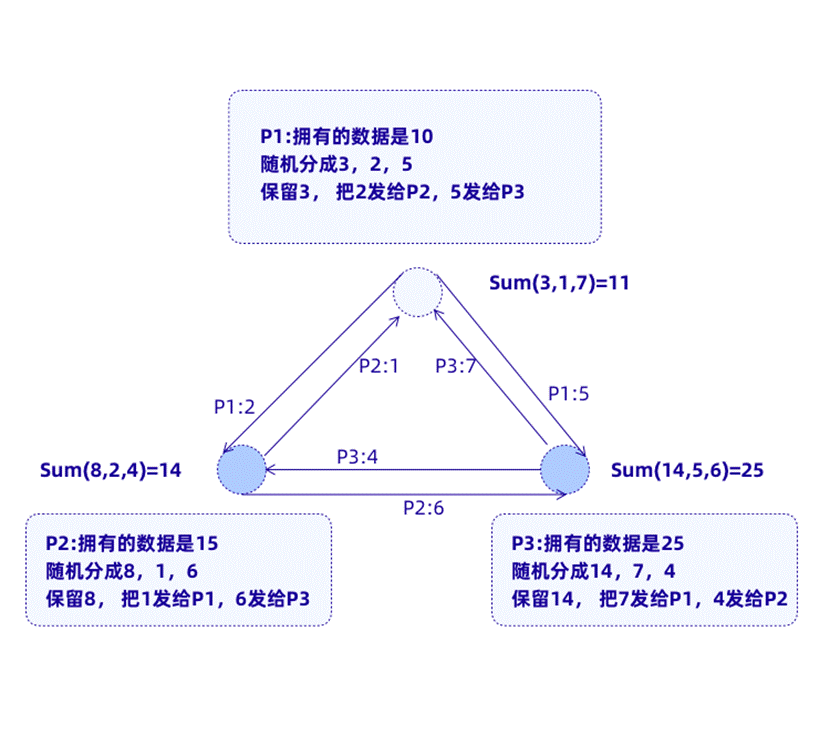
如上图所示，假设我们的目标是联合计算各方所有秘密数据的总和，这可以通过秘密共享来实现。

首先，每一方将其秘密号码随机分成三部分，并将其中两部分别分享给其他部分。

然后，每一方在本地对来自其他对等方及其自身的所有分享秘密进行汇总加和处理。为了公开最终结果，每个方的本地总和（local sum）都会公开给同行（Peers）。

最后，任何一方都可以将所有公共本地总和相加来得知最终结果。

 

秘密共享的关键点在于，通过了解秘密共享，一方不会获知有关私有数据的信息。例如，在通过揭示秘密共享5的三方计算中，秘密数据可以是10、79、-11这样的随机数字。即使知道秘密共享，该方也可以猜测私人数据，而不是猜测随机数。   

由于整个过程没有显示隐私数据，因此秘密共享计算可以保护隐私，对手方无法发现秘密信息。

以上是一个简单的例子。在秘密分享邻域，也涌现出许多种方案，最著名的是图灵奖得主 Adi Shamir 的《How to Share a Secret》，里面有非常漂亮的算法。

 

2.3.5     Private Set  Intersect - PSI （隐私保护集合交集）

 

隐私保护集合交集协议允许持有各自集合的两方共同计算两个集合的交集运算。在协议交互的最后，一方或是两方应该得到正确的交集，而且不会得到交集以外另一方集合中的任何信息。保护集合的隐私性在很多场景下是自然甚至是必要的需求，比如当集合是某用户的通讯录或是某基因诊断服务用户的基因组，这样的输入就一定要通过密码学的手段进行保护。

如果数据量相对较小，我们可以采用多重加密或salt来实现交集计算。对于数据量大的情况，则需要多种技术进行融合，譬如采用基于安全布隆过滤器的技术等。

 

 

2.3.5.1     Private Information Retrieve - PIR （隐私信息获取）

 

隐私信息获取是一种从数据库/数据源中查询所需信息，同时又不让数据源拥有者获得查询条件的一种方法。例如，当银行客户需要通过用户的身份证信息从某个外部数据源处查询用户的其他相关信息（譬如消费情况），同时又不希望透露用户的身份证信息，就需要用到PIR技术。

 

最朴素的方式是数据拥有方把全部或者一段范围用户的信息发送给请求方，然后请求方在自己的系统内做匹配查询，这种称为“琐碎下载” *(Trivial Download)。 当然，数据拥有方肯定也希望被下载的数据范围越小越好，毕竟数据转移后价值也被转移了。从类型上可分为计算型隐私信息获取(Computational PIR) 和信息理论型信息获取，前者主要通过算法的复杂性节省服务器的成本（一般可以采用单服务器），而后者则通过多台服务器将请求条件分散到每台服务器上，然后再将这些信息拼起来，使每台服务器都只能得到不完整的查询条件，同时也无法简单复原。^[5] 

 

2.3.6    联邦学习

 

联邦学习是一种数据保护下基于机器学习的建模和推导技术，最终在保护各自数据的基础上实现数据的联合价值挖掘。举例来说，假设有两个不同的企业A和B，它们拥有不同的数据，比如企业A有用户特征数据，企业B有产品特征数据和标注数据。根据GDPR准则，这两家企业是不能“粗暴”地把双方数据加以合并的，因为他们各自的用户并没有同意这样做。假设双方各自建立一个任务模型，对每个任务进行分类或预测，这些任务也已经在数据获取阶段取得了各自用户的认可。那么，现在的问题是如何在A和B各端建立高质量的模型。但是，由于数据不完整（例如企业A缺少标签数据，企业B缺少特征数据），或者数据不充分（数据量不足以建立好的模型），各端都有可能无法建立模型或效果不理想。联邦学习的目的是解决这个问题：它希望做到各个企业的自有数据不出本地，联邦系统可以通过加密机制下的参数交换方式，在不违反数据隐私保护法规的情况下，建立一个虚拟的共有模型。这个虚拟模型就像我们通过聚合数据构建的最优模型一样。但是在建立虚拟模型的时候，数据本身不会移动，也不会泄露用户隐私或影响数据的规范化。这样，建好的模型仅为各自区域的本地目标服务。在这样的联邦机制下，各个参与方都有相同的身份和地位，而联邦系统帮助大家建立了“共同富裕”的战略。^[6] 

 

3    总结

 

在数字化时代、大数据时代、智能时代，如何在保障数据安全的前提下让数据充分发挥价值？这是目前大数据产业发展中最大的痛点。如果这个问题得不到解决，将极大地限制大数据产业的发展。令人欣慰的是，业界正在积极探索解决这一矛盾，并取得了一定成绩：在融合多方安全计算、区块链等多种技术上，形成多层链/网络、计算网络和存证链、智能合约平台以及通证化。在大家的共同努力下，我们有信心在这个方向上取得突破，让产业能够持续健康发展。

 

 

参考文献：

[1] 国际电信联盟(ITU)制定的5G 标准

[2] 中信出版集团 ISBN978-7-5086-6685-3 《区块链革命》 第二章

[3] 浙江人民出版社 ISBN978-7-213-05254-5 《大数据时代》

[4] 阿里首次实现“公开可验证” 的安全方案 https://yq.aliyun.com/articles/693332

[5] Casey Devet, Ian Goldberg, Nadia Heninger.  Optimally Robust Private Information Retrieval

[6] 杨强,刘洋,陈天健,童咏昕.  联邦学习，计算机学会通讯第14卷第11期